2.4 색인과 슬라이싱 기초

데이터의 부분집합이나 개별 요소를 선택하는 방법은 정말 다양하다. 1차원 배열은 단순하며, 표면적으로는 파이썬의 리스트와 유사하게 동작한다.

IN

GD_arr = np.arange(15)
GD_arr

OUT

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

IN

GD_arr[3]

OUT

3

IN

GD_arr[3:7]

OUT

array([3, 4, 5, 6])

IN

GD_arr[3:7] = 7
GD_arr

OUT

array([ 0,  1,  2,  7,  7,  7,  7,  7,  8,  9, 10, 11, 12, 13, 14])

GD_arr[3:7] = 7처럼 배열 조각에 스칼라값을 대입하면 7이 선택 영역 전체로 전파된다. 리스트와의 중요한 차이점은 배열 조각은 원본 배열의 뷰라는 점이다. 다시 말하자면, 데이터는 복사되지 않고 뷰에 대한 변경은 그대로 원본 배열에 반영된다. 이해를 돕기 위해 GD_arr 배열의 슬라이스를 생성해 보겠다.

IN

GD_arr_slice = GD_arr[3:7]
GD_arr_slice

OUT

array([7, 7, 7, 7])

GD_arr에서 7로 변경된 영역 전체를 GD_arr_slice라는 이름의 새로운 배열로 만들었다.

IN

GD_arr_slice[1] = 3333
GD_arr

OUT

array([   0,    1,    2,    7, 3333,    7,    7,    7,    8,    9,   10,
      11,   12,   13,   14])

위 코드처럼 GD_arr_slice의 값을 변경하면 원래 배열인 GD_arr의 값도 바뀌어 있음을 확인할 수 있다.

IN

GD_arr_slice[:] = 33
GD_arr

OUT

array([ 0,  1,  2, 33, 33, 33, 33,  7,  8,  9, 10, 11, 12, 13, 14])

범위를 [:] 형태로 주게 되면 배열의 모든 값을 의미하는데, 위 코드처럼 GD_arr_slice의 값을 33으로 변경하게 되면 원래 배열의 값이 변경된 것을 다시 한번 확인할 수 있다.

Numpy를 처음 접한다면, 다른 배열 프로그래밍 언어와 다르게 데이터가 복사되지 않는다는 점에 놀랄 것이다. 이런 점이 Numpy를 데이터 처리에 사용해야 하는 이유다. 만약 Numpy가 데이터 복사를 남발한다면 성능과 메모리 문제에 마주치게 될 것이다.

그렇다고 뷰 대신 슬라이스의 복사본 값을 만들지 못하는 것은 아니다. GD_arr[3:7].copy()를 사용해서 명시적으로 배열을 만들면 가능하다. copy() 명령은 조금 이따 살펴보도록 하자.

IN

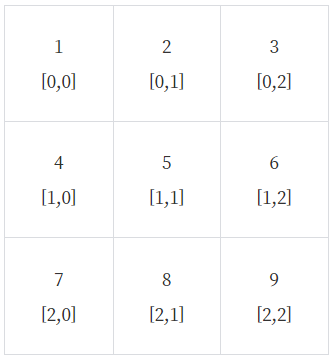
GD_arr2d = np.array([[1,2,3],[4,5,6],[7,8,9]])
GD_arr2d

OUT

array([[1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])

IN

GD_arr2d[1]

OUT

array([4, 5, 6])

다차원 배열을 다룰 때는 좀 더 많은 옵션이 있다. 2차원 배열에서 각 색인에 해당하는 요소는 스칼라 값이 아니라 1차원 배열이라는 점을 기억하자.

IN

GD_arr2d[0][1]

OUT

2

IN

GD_arr2d[0,1]

OUT

2

따라서 개별 요소는 재귀적으로 접근해야 하는데, 콤마로 구분된 색인 리스트를 넘기면 동일한 값이 출력된다.

이해를 돕기 위해 GD_arr2d 배열에서의 값들을 색인과 함께 그려 보았다.

IN

GD_arr3d = np.array([[[1,2,3],[4,5,6]],[[7,8,9],[10,11,12]]])
GD_arr3d

OUT

array([[[ 1,  2,  3],
     [ 4,  5,  6]],

    [[ 7,  8,  9],
     [10, 11, 12]]])

IN

GD_arr3d[0]

OUT

array([[1, 2, 3],
    [4, 5, 6]])

3차원의 배열을 만들고 색인 값에 0만 넣어서 출력해 보았다. 다차원 배열에서 마지막 색인을 생략하면 반환되는 객체는 상위 차원의 데이터를 포함하고 있는 한 차원 낮은 ndarray가 된다. GD_arr3d[0]은 2x3 크기의 배열이다.

IN

GD_values = GD_arr3d[0].copy()
GD_arr3d[0] = 42
GD_arr3d

OUT

array([[[42, 42, 42],
     [42, 42, 42]],

    [[ 7,  8,  9],
     [10, 11, 12]]])

IN

GD_arr3d[0] = GD_values
GD_arr3d

OUT

array([[[ 1,  2,  3],
     [ 4,  5,  6]],

    [[ 7,  8,  9],
     [10, 11, 12]]])

copy() 명령어를 활용하여 GD_values에 GD_arr3d[0]의 값을 복사했다. 그리고 GD_arr3d[0]에 스칼라값과 배열 모두 대입할 수 있다는 것을 확인할 수 있다.

IN

GD_arr3d[1,0]

OUT

array([7, 8, 9])

IN

s = GD_arr3d[1]
s

OUT

array([[ 7,  8,  9],
    [10, 11, 12]])

IN

s[0]

OUT

array([7, 8, 9])

이런 식으로 GD_arr3d[1,0]은 (1,0)으로 색인되는 1차원 배열과 그 값을 반환한다. 이해를 돕기 위해 s를 활용하여 두 번의 인덱싱으로 표현해 봐도 결과는 동일하다.

이제 슬라이스로 배열의 객체들을 선택해 보겠다.

IN

GD_arr

OUT

array([ 0,  1,  2, 33, 33, 33, 33,  7,  8,  9, 10, 11, 12, 13, 14])

IN

GD_arr[1:6]

OUT

array([ 1,  2, 33, 33, 33])

파이썬의 리스트 같은 1차원 객체처럼 ndarray는 익숙한 문법으로 슬라이싱이 가능하다.

IN

GD_arr2d

OUT

array([[1, 2, 3],
    [4, 5, 6],
    [7, 8, 9]])

IN

GD_arr2d[:2]

OUT

array([[1, 2, 3],
    [4, 5, 6]])

GD_arr2d[:2]는 첫 번째 축인 0번 축을 기준으로 슬라이싱 되었다. 따라서 슬라이스는 축을 따라 선택 영역 내의 요소를 선택한다. GD_arr2d의 시작부터 두 번째 행까지의 선택으로 이해하면 된다.

IN

GD_arr2d[:2,1:]

OUT

array([[2, 3],
    [5, 6]])

색인을 여러 개 넘겨서 다차원을 슬라이싱하는 것도 가능한데, 이렇게 슬라이싱하면 항상 같은 차원의 배열에 대한 뷰를 얻게 된다.

IN

GD_arr2d[0, :2]

OUT

array([1, 2])

정수 색인과 슬라이스를 함께 사용해서 한 차원 낮은 슬라이스를 얻을 수도 있다. 첫 번째 행에서 처음 두 열만 선택한 결과이다.

IN

GD_arr2d[:2,2]

OUT

array([3, 6])

처음 두 행에서 세 번째 열만 선택한 결과이다.

IN

GD_arr2d[:,:1]

OUT

array([[1],
    [4],
    [7]])

그냥 콜론만 쓰면 전체 축을 선택한다는 의미이므로 이렇게 하면 원래 차원의 슬라이스를 얻게 된다.

IN

GD_arr2d[:2,1:] = 7
GD_arr2d

OUT

array([[1, 7, 7],
    [4, 7, 7],
    [7, 8, 9]])

이렇게 슬라이싱한 구문에 값을 대입하면 선택 영역 전체에 값이 대입된다.

마지막으로 이해를 돕기 위해 추가적으로 2가지의 슬라이싱을 해보았다.

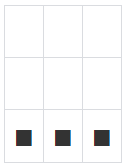
GD_arr[2] , GD_arr[2, :] , GD_arr[2:, :]의 코드 형태로 표현이 가능하다.

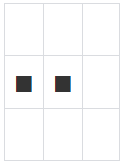
GD_arr[1, :2] , GD_arr[1:2, :2]의 코드 형태로 표현이 가능하다.

글을 여기서 마치고, 다음에는 불리언값을 활용해서 데이터를 선택하는 방법을 알아보도록 하자.